위상정렬(Topological Sort)

Example of topological sort

어떤 연속적이지만 특정한 순서가 있는 테스크들에 우리는 topological sort를 적용할 수 있습니다. 예를들면 옷을 입고 학교를 가는것을 예제로들자면 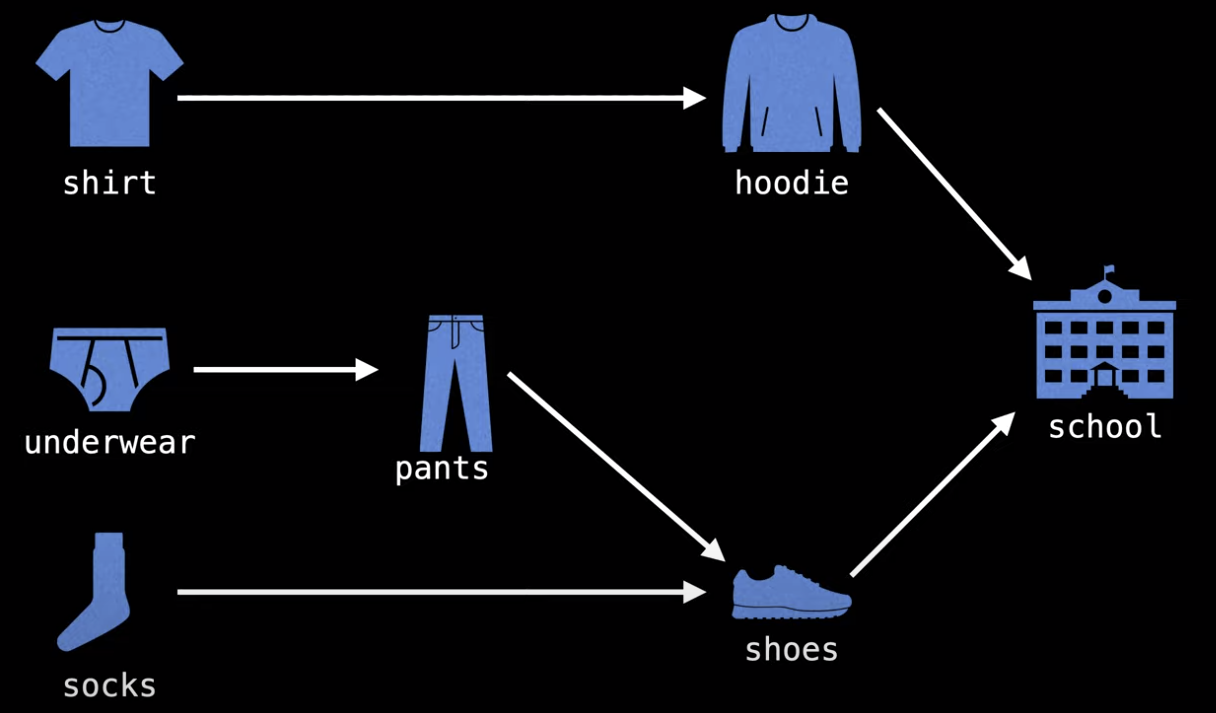셔츠, 속옷, 양말중 어떤것을 먼저 입느냐는 중요하지 않지만 바지를 입기전에 속옷을 입는다던지 아님 양말을 신기전 신발을 신는 행동들은 이상한 결과를 가져올것 입니다. 따라서 결과적으로 유일하진(unique) 않지만 특정한 순서가 존재하는것은 분명하고 위예제에서 가능한 topological ordering은 다음과 같을 것입니다.

다수의 많은 상황들이 위예제와 같이 방향그래프(directed graph)를 사용하여 표현될 수 있습니다. 예를들면, program build dependencies, college class prerequisites, event scheduling, assembly instruction 등이 위상정렬을 통해 표현될 수 있을것 입니다.

정의

위상정렬이란 방향그래프의 노드에 대한 정렬입니다.

대표적으론 Kahn’s algorithm이 있고 이를 수행하였을경우 O(V+E) 시간복잡도안에 위상정렬을 수행할 수 있습니다. 주위해야할 내용으론 위상정렬은 고유한 값을 가지고 있지 않습니다. 이는 다양한 결과값이 존재할 수 있다는것을 알려줍니다.

조건

모든 그래프문제가 위상정렬문제에 적합하진 않습니다. 오로직 DAGs(directed acyclic graphs)만이 정확한 결과 값을 얻을 수 있습니다. 즉 방향그래프이면서 사이클이 없을떄 가능합니다.

Kahn’s algorithm

전반적인 알고리즘은 우선 반복적으로 다른하나에 종속되지 않은 노드들을 그래프에서 제거한후 결과값에 추가해주는 것입니다.

예제를 하나 보겠습니다.

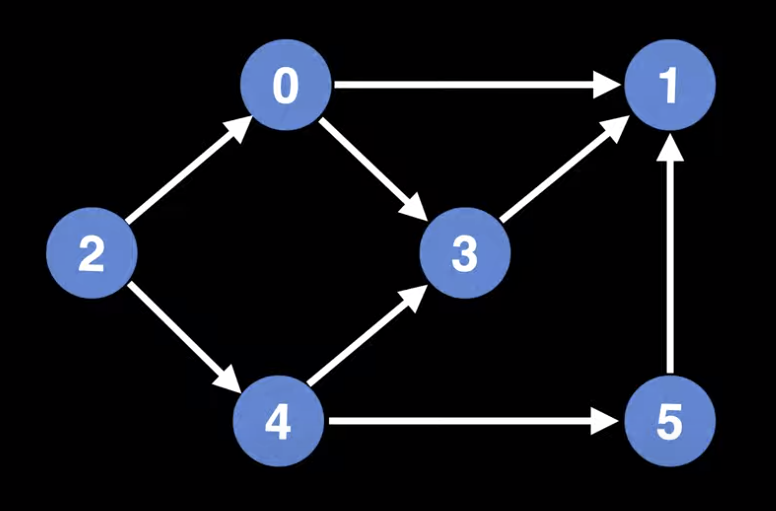
독립적인 노드란, 노드에 들어오는 in-order가 0이란 말과 비슷합니다. 그래프에 이와 같은 노드들을 찾은후에 전부 큐에 넣어줍니다. 이렇게 하면 가장먼저 노드 2가 큐에 들어올 것입니다. 이를 그래프에서 제거한후 기존에 종속되었던 노드0과 노드4에 대해서도 결과를 반영해줍니다. 그리고 만약 노드 0과 4가 이로인해 독립적인 노드가 되었다면 이를 다시 큐에 넣어주는 형식으로 반복합니다. 이를 수행했을경후 하나의 가능한 위상정렬은 [2, 0, 4, 3, 5, 1] 입니다.

코드

vector<int> FindTopologicalOrdering(g)
{
    // 그래프의 각노드에 대해 inorder를 계산함
    n = g.size();
    vector<int> in_degree(n);
    for(int i=0; i<n; ++i)
    {
        for(auto& to : g[i])
        {
            in_degree[to] = in_degree[to] + 1;
        }
    }

    //인오더의 값이 0인 경우 즉 독립적인 노드만 큐에 넣어준다
    queue<int> q;
    for(int i =0; i<n; ++i)
    {
        if(in_degree[i] == 0)
        {
            q.push(i);
        }
    }

    /*
        1. 큐를 확인하여 독립적인 노드들에 대해 작업을 수행한다.
        2. 해당노드를 결과에 추가시킨다.
        3. 기존에 해당노드에 종속받았던 노드들의 인오더 값을 제거해준다
        4. 더이상 종속되지 않은 노드들은 큐에 추가해준다.
        이를 반복한다.
    */
    int index = 0;
    vector<int> order(n);
    while(!q.empty())
    {
        int at = q.front();
        q.pop();
        order[index++] = at;
        for(auto to:g[at])
        {
            in_degree[to] = in_degree[to]-1;
            if(in_degree[to] == 0)
            {
                q.push(to);
            }
        }
    }

    // index 값이 노드의 수와 같지 않다는것은 사이클이 존재한다는것을 의미합니다.
    // 만약 A->B->C->A 의 그래프가 있다고 가정했을 경우 어떠한 노드노 큐에 추가되지 않습니다. 따라서 인덱스 값을 n이 될 수 없습니다.
    if(index != n)
    {
        return NULL;
    }
    return order; 
}

Reference

1. 이 노트는 topological sort를 참고 했습니다.